Aritalab:Lecture/NetworkBiology/Percolation on Graph
From Metabolomics.JP
| Wiki Top | Up one level | レポートの書き方 | Arita Laboratory |
|
グラフ上のパーコレーション
グラフをある次数分布に従うツリーとみなすことで、パーコレーションを扱ってみます。ここでの議論は母関数を使った説明もあります。
あるネットワークの平均次数が <k> で与えられるとき、隣接点の平均次数は 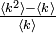 になります。この本数のうち、確率 q でサイトが ON になる場合、隣接点の周りで占有される頂点数は
になります。この本数のうち、確率 q でサイトが ON になる場合、隣接点の周りで占有される頂点数は 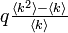 になります。これが 1 を上回る場合に相転移をおこすので、臨界確率
になります。これが 1 を上回る場合に相転移をおこすので、臨界確率 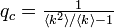 が得られます。つまり、<k2> / <k> のバランスに臨界確率が左右されるということです。
が得られます。つまり、<k2> / <k> のバランスに臨界確率が左右されるということです。
パーコレーションの起こりやすさ
いかなる次数分布でも、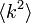 が
が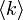 に比して大きいと、低い浸透確率で相転移が起こります。
に比して大きいと、低い浸透確率で相転移が起こります。
格子グラフ、Erdosブラフ
次数が一定の場合、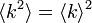 です。すなわち、
です。すなわち、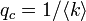 となります。
となります。
次数分布がポアソン分布をなす場合、平均と分散は等しく ![E[k] = V[k] = \langle k \rangle](/mediawiki/images/math/a/0/8/a08c7b8e48d6939e5f49fc09c58327bc.png) になります。
このとき
になります。
このとき 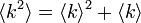 です。この場合も格子グラフとほぼ同じで、平均次数に反比例して浸透確率が下がります。
です。この場合も格子グラフとほぼ同じで、平均次数に反比例して浸透確率が下がります。
スケールフリーネットワーク
次数の分布が、べき分布 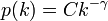 のときをかんがえましょう。
ここで
のときをかんがえましょう。
ここで 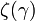 はリーマンゼータ関数とします。
はリーマンゼータ関数とします。
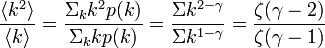
この値は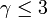 のときに発散します。また
のときに発散します。また 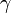 が大きくなると
が大きくなると 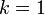 の項が大きな要素を占めるのでほとんど 1 に近づきます。
の項が大きな要素を占めるのでほとんど 1 に近づきます。