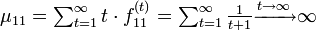Aritalab:Lecture/NetworkBiology/Markov Chains
| Wiki Top | Up one level | レポートの書き方 | Arita Laboratory |
|
ここではランダムウォークを考えるのに便利な概念を導入します。
マルコフ連鎖
離散確率過程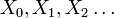 は
は
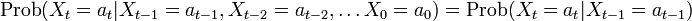
を満たすときにマルコフ連鎖 (Markov chain) と呼ばれます。マルコフとはロシアの統計学者 Andrei A. Markov (1856-1922) のことで、マルコフ連鎖に関する多くの功績を残しました。状態 (state) 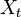 が状態
が状態 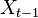 のみに依存して決まる性質をマルコフ性 (Markov property) または無記憶性 (memoryless property) といいます。
のみに依存して決まる性質をマルコフ性 (Markov property) または無記憶性 (memoryless property) といいます。
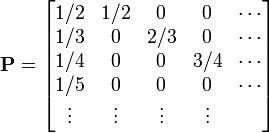
マルコフ連鎖において状態 i から j への遷移確率を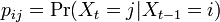 と書けば、マルコフ連鎖は遷移行列
と書けば、マルコフ連鎖は遷移行列
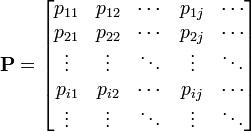
で記述できます。[1] 遷移確率を表すので行列の行方向に足し合わせた値は必ず 1 になっており、確率行列 (stochastic matrix) と呼ばれます。もし行方向に足し合わせても 1 になる場合、二重確率行列 (doubly stochastic matrix) と呼ばれます。
記法を拡張し、i から j へ正確に m ステップで移る遷移確率を
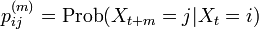
と書きましょう。右肩にある (m) という表記は、m ステップ後という意味で m 乗ではありません。1ステップ目で移動した先を k と書くと
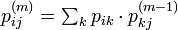 であるから、遷移行列
であるから、遷移行列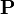 を m 乗すれば正確に m ステップで移った先を示す遷移行列を得ます(数学的帰納法)。また記法をそろえるために
を m 乗すれば正確に m ステップで移った先を示す遷移行列を得ます(数学的帰納法)。また記法をそろえるために
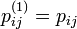
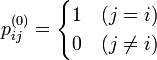
と定義します。
チャップマン-コルモゴロフの等式
m ステップの遷移を、 s ステップと m − s ステップに分解する以下の式は、チャップマン-コルモゴロフの等式と呼ばれます[2]。
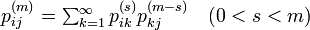
以下でも 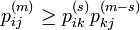 という式をよく使います。
という式をよく使います。
既約
状態 i から j へ何ステップかで到達できる場合、j は i から到達可能 (accessible) と呼びます。
互いに到達可能な状態 i, j どうしを連結 (communicate) しているといい、 と書きます。連結性により同値類が形成されます。
と書きます。連結性により同値類が形成されます。
- 反射律 (reflexivity): いかなる状態 i も、
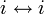
- 対称律 (symmetry):
 なら
なら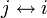
- 推移律 (transitivity):
 かつ
かつ なら
なら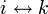
全ての状態が同じ同値類 (communication class) に属すとき、つまり全ての頂点が互いに連結なとき、マルコフ連鎖は既約 (irreducible) といいます。既約なマルコフ連鎖とは、グラフ表現すると強連結 (strongly connected) になっていて、任意の頂点から任意の頂点に移動できる場合に相当します。
また、状態集合 C は、C に属すどの状態からも C 以外の状態に抜け出せないとき、閉じている (closed) といいます。例えば、グラフ表現した際に外に出る辺をもたない状態だけからなる集合は閉じています。
- 例: 1次元のウォーク
0 と N の間を左右に1ステップずつ移動し、0, N を吸収状態とするランダムウォークを考えます。0 から N までの状態は 3 つの同値類 {0}, {1, 2, ..., N−1}, {N} に分かれ、{0, N} は閉じています。
周期性
状態 i に戻ってくるまでのステップ数が自然数 k (>1) の倍数回に限られ、しかも k がこの性質を持つ最大公約数の場合、状態 i は周期 k でといいます。 k = 1 のとき、状態は非周期的であるといいます。マルコフ連鎖の中で同じ同値類に属する (communicativeな) 状態 i, j は同じ周期をもちます[3]。
- 例:円周上のウォーク
円周上に配置された N 状態が一方向につながったマルコフ連鎖は、規約で周期 N を持ちます。遷移行列 P を N 乗すると、恒等行列 I になります。
- 例: 1次元のウォーク
原点からスタートして左右に1ステップずつ移動するウォークでは、原点に戻るまでのステップ数が必ず偶数です。つまり、状態 0 は周期 2 になります。いずれの状態も周期は 2 です。
再帰性
状態 i から出発し時刻 t になって初めて j に到達する確率を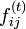 と書くことにします。
前出の
と書くことにします。
前出の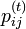 は複数回 j を訪れることを許すため、
は複数回 j を訪れることを許すため、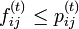 となります。
となります。
再帰時間
同じ状態に初めて戻る確率 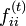 を初再帰確率 (first return probability) と呼び
を初再帰確率 (first return probability) と呼び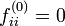 と定義します。状態 i は
と定義します。状態 i は
-
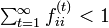 であれば再帰不確実 (transient)
であれば再帰不確実 (transient)
-
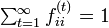 であれば再帰確実 (recurrent)
であれば再帰確実 (recurrent)
と呼びます。全ての状態が再帰確実であれば、マルコフ連鎖自体を再帰確実と呼びます。
平均初再帰時間 MFRT
状態 i における平均初再帰時間 (mean first return time または mean recurrence time) を
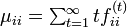
と書きます。状態 i が再帰不確実な場合は 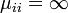 です。
です。
状態 i が再帰確実でも 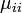 が有限とは限りません。初再帰時間の期待値が有限なとき有限再帰 (positive recurrent)、そうでない場合をゼロ再帰 (null recurrent) と呼びます。ゼロ再帰性を満たすには無限の状態数が必要です。
が有限とは限りません。初再帰時間の期待値が有限なとき有限再帰 (positive recurrent)、そうでない場合をゼロ再帰 (null recurrent) と呼びます。ゼロ再帰性を満たすには無限の状態数が必要です。
- 例:2 × 2 行列
以下の確率行列を持つ 2 状態のマルコフ連鎖は有限再帰的です。
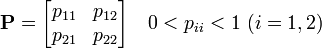
直感的には 2 状態の間を自由に行き来できるため、必ず戻ってきます[4] 。
- 例:ゼロ再帰的なマルコフ連鎖
正の整数値に対応するマルコフ連鎖を仮定し、状態 i から確率 i/(i + 1) で状態 i + 1 に、確率 1/(i + 1) で状態 1 に移動するとします。
高い確率で無限遠に進んでいけるため、状態 1 に初めて戻るまでの期待値は無限大でゼロ再帰的です[5]。
通過時間、平均初通過確率 MFPT
状態 i から始めて j に最初に訪れる確率 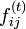 を初通過確率 (first passage time probability) と呼び、
を初通過確率 (first passage time probability) と呼び、 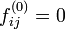 と定義します。平均初通過時間 (mean first passage time; MFPT) も同様に定義します。
と定義します。平均初通過時間 (mean first passage time; MFPT) も同様に定義します。
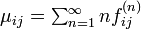
定常分布
マルコフ連鎖の遷移行列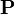 に対して
に対して
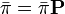
を満たし、要素の総和が 1 、つまり 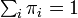 となるような行ベクトル
となるような行ベクトル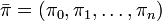 を定常分布 (stationary distribution) といいます。定常分布は PT の固有値 1 に対応する固有ベクトルともみなせます。状態数が有限の場合は 1 を必ず固有値に持つので定常分布が存在しますが、ただ一つに定まるとは限りません。
を定常分布 (stationary distribution) といいます。定常分布は PT の固有値 1 に対応する固有ベクトルともみなせます。状態数が有限の場合は 1 を必ず固有値に持つので定常分布が存在しますが、ただ一つに定まるとは限りません。
- 例:無限個の定常分布を持つマルコフ連鎖
確率行列が n 次元の単位行列 I のとき、定常状態は無限にあります。固有値 λ (n個) は全て 1 で、このマルコフ連鎖は既約ではありません (reducible)。
- 例:定常分布を持たないマルコフ連鎖
正の整数値に対応するマルコフ連鎖を仮定し、状態 i から i, i + 1, i + 2 ... にそれぞれ 1/2, 1/4, 1/8 ... の確率で遷移するとします。各状態が再帰不確実なため、定常状態 π はゼロベクトルになってしまいます。
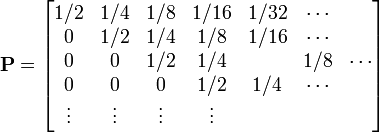
定常分布をもつ条件
既約で、再帰確実かつ非周期的(エルゴード的)なマルコフ連鎖は唯一つの定常分布 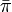 を持ち、 再帰時間の期待値との間に
を持ち、 再帰時間の期待値との間に
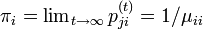
が成り立ちます。この証明および関連する定理は、定常分布のページを参照してください。
これは再帰時間の期待値が出発する状態 j に依存しないことを意味し、再帰までのステップ数期待値が 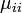 ならば状態 i に戻ってくる確率が
ならば状態 i に戻ってくる確率が 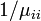 であることに対応します。定常状態において、各状態での存在確率は出発点に依存しません。
であることに対応します。定常状態において、各状態での存在確率は出発点に依存しません。
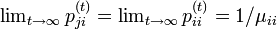
さらに定常分布においては、各状態に入る確率と出る確率が等しいことにも注意します。
つまり全ての状態 i, j に対し、i から出ていく確率の和は、i に入ってくる確率の和に等しく 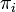 になります。
になります。
エルゴード的であれば定常分布がただ一つに定まることを証明しましょう。
仮に定常分布が二つあるとして、もう一つの分布を  と書きます。
定常分布であるから
と書きます。
定常分布であるから
すなわち です。
です。
参考・解説
- ↑ 状態 i から j への遷移確率を pij とする記法が主流ですが (Karlin & Taylor 1975)、Linda JS Allen (2011 2nd Ed) では j から i への遷移確率を pij と定義しています。そうすると定常分布を考える際に 以下で書くように行ベクトル π を用いて
 とするのではなく、列ベクトルを用いて
とするのではなく、列ベクトルを用いて 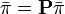 と書けるようになります。記法上の問題であり、本質はかわりません。
と書けるようになります。記法上の問題であり、本質はかわりません。
- ↑
- チャップマン-コルモゴロフの等式の証明
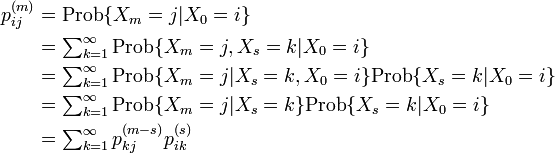
- ↑
- 同じ同値類に属する状態の周期が等しいことの証明
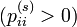 、d(i) は s を割り切ります。 i と j が同値類に属する場合、 i → j を m ステップ、 j → i を n ステップで移動することが可能
、d(i) は s を割り切ります。 i と j が同値類に属する場合、 i → j を m ステップ、 j → i を n ステップで移動することが可能 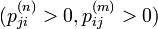 ですから
ですから
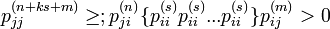 となります。状態 j の周期は (n + ks + m) をどんな正の整数 k に対しても割り切るので、s も割り切ります。ここから d(j) ≤ d(i) が導かれます。同様の議論で d(i) ≤ d(j) も成り立つので d(i) = d(j) となります。
となります。状態 j の周期は (n + ks + m) をどんな正の整数 k に対しても割り切るので、s も割り切ります。ここから d(j) ≤ d(i) が導かれます。同様の議論で d(i) ≤ d(j) も成り立つので d(i) = d(j) となります。
- ↑
- 例:2 × 2 行列が正再帰的になることの証明
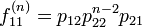 が成立します。状態 1 の再帰確率は 1 になります。状態 2 についても同じです。しかし平均初再帰時間は有限になります。
が成立します。状態 1 の再帰確率は 1 になります。状態 2 についても同じです。しかし平均初再帰時間は有限になります。
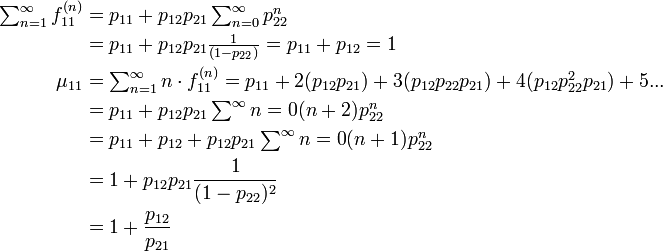
- ↑
- ゼロ再帰性の証明
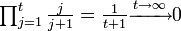 したがって状態 1 は再帰確実
したがって状態 1 は再帰確実 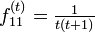 (t − 1 ステップ 1 に戻らず、t ステップ目で 1 に戻る)。しかし、状態 1 に初めて戻るまでの期待値は無限大なので、ゼロ再帰。
(t − 1 ステップ 1 に戻らず、t ステップ目で 1 に戻る)。しかし、状態 1 に初めて戻るまでの期待値は無限大なので、ゼロ再帰。