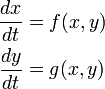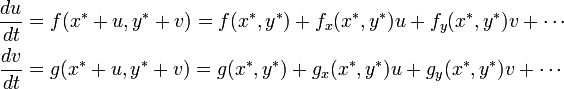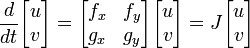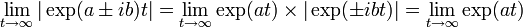Aritalab:Lecture/Bioinformatics/Stability

安定性解析

一般的な微分方程式系を考えます。

$\begin{align} \frac{dx}{dt} &= f(x, y)\\ \frac{dy}{dt} &= g(x, y) \end{align}$

定常状態を (x^*, y^*) とし、そこから少しずれた位置の挙動を調べます。それには (x^* + u, y^* + v) とした差分 u , v をテイラー展開します。ずれが微小であることから2次以上の部分は無視します。

$\begin{align} \frac{du}{dt} &= f(x^* + u, y^* + v) = f(x^*, y^*) + f_x(x^*, y^*)u + f_y(x^*, y^*)v + \cdots \\ \frac{dv}{dt} &= g(x^* + u, y^* + v) = g(x^*, y^*) + g_x(x^*, y^*)u + g_y(x^*, y^*)v + \cdots \end{align}$

これを行列の形に書くと

$\frac{d}{dt}\begin{bmatrix} u \\ v \end{bmatrix} = \begin{bmatrix} f_x & f_y \\ g_x & g_y \end{bmatrix} \begin{bmatrix} u \\ v \end{bmatrix} = J \begin{bmatrix} u \\ v \end{bmatrix}$

ここで行列 J をヤコビ行列といいます。

ヤコビ行列

線形微分方程式はヤコビ行列 J の固有値 λ₁, λ₂ を用いた解があります。

λ₁ ≠ λ₂ のとき

$\begin{bmatrix} u \\ v \end{bmatrix} = \begin{bmatrix} c_{11} \\ c_{21} \end{bmatrix} \exp(\lambda_1 t) + \begin{bmatrix} c_{12} \\ c_{22} \end{bmatrix} \exp(\lambda_2 t)$

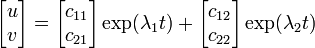
λ₁ ＝ λ₂ ＝ λ のとき

$\begin{bmatrix} u \\ v \end{bmatrix} = \begin{bmatrix} c_{11} \\ c_{21} \end{bmatrix} \exp(\lambda t) + \begin{bmatrix} c_{12} \\ c_{22} \end{bmatrix} t \exp(\lambda t)$

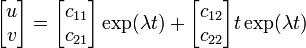
いずれの場合でも以下の議論は同じなため、一緒に扱いましょう。 固有値が実数の時、λ₁ < 0, λ₂ < 0 であれば、平衡点からの差分 u , v は時間とともに 0 に収束します。どちらかでも正であれば、差分は発散します（つまり線形近似は成り立たなくなります）。 固有値が複素数の時、２つの固有値は複素共役になり λ₁, λ₂ = a ± i b です。虚数の exp は絶対値が 1 になることを利用して

$\lim_{t \rightarrow \infty}| \exp(a \pm ib)t | = \lim_{t \rightarrow \infty} \exp(at) \times | \exp(\pm ibt) | = \lim_{t \rightarrow \infty} \exp(at)$

ですから、固有値の実部が共に負であれば、平衡点からの差分はやはり 0 に収束することがわかります。 この議論は多元連立の場合もそのまま成立します。

まとめると、

• 固有値の実部が全て負であれば、平衡点は局所安定
• 固有値の実部が一つでも正であれば、平衡点は不安定
  • 全て正の時は全方向に発散する不安定点 (unstable node)
  • 正と負が両方ある場合、方向によって一部収束する鞍点 (saddle node)

となります。固有値が複素数の時は近傍で周期的な挙動（スパイラル）をみせながら収束（安定フォーカス）または発散（不安定フォーカス）します。

Routh-Hurwitz 条件

2 x 2 行列 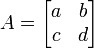$A = \begin{bmatrix} a & b\\ c & d\end{bmatrix}$ の固有値実部が負であるための必要十分条件は tr(A) = a + d < 0 かつ det(A) = ad - bc > 0 になります。