Aritalab:Lecture/NetworkBiology/Random Walk/Reflection
m (→ギャンブラーの破産問題) |
m (→ギャンブラーの破産問題) |
||
| Line 39: | Line 39: | ||
==ギャンブラーの破産問題== | ==ギャンブラーの破産問題== | ||
| − | |||
| − | + | コインを ''i'' 枚持つギャンブラーが確率 ''p'' で表の出るコインを投げ、表がならコインを 1 枚受け取り、裏なら 1 枚失います。コインを全て失う前に ''n'' 枚に増える確率を考えましょう。 | |
| − | + | ||
| − | + | これは確率 ''p'' − 1, ''p'' で左右にそれぞれ 1 移動し、位置 0 と ''n'' を吸収壁とみなしたランダムウォークです。位置 0 が破産、位置 ''n'' を勝ちとみなして、位置 ''i'' における勝率を考えます。 | |
| − | + | 勝率が満たす漸化式は | |
| − | + | <math> | |
| + | P(i) = p P(i-1) + (1-p) P(i+1)\, | ||
| + | </math> | ||
| − | <math> | + | です。 <math>P(i)\,</math>を求めましょう。 |
| − | + | ; p = 1/2 のとき | |
| + | 左右に公正に移動するウォークなので、漸化式を満たす<math>P(i)\,</math>として等差数列 <math>\,ai + b</math> を仮定できます。境界条件<math>P(0) = 0\,</math>, <math>P(n) = 1\,</math>から <math>P(i) = i/n\,</math> です。 | ||
| − | <math> \ | + | ; p ≠ 1/2 のとき |
| + | 左右に移動するたびに <math>p/(1-p)\,</math>倍に勝率が変わるウォークなので、漸化式から<math>P(i)\,</math>が等比数列 <math>\,ak^i + b</math> と予測できます。これを漸化式に代入しましょう。 | ||
| − | + | <math> | |
| − | + | \begin{align} | |
| + | k^i &= p k^{i-1} + (1-p)k^{i+1}\\ | ||
| + | k &= p + (1-p) k^2 | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |||
| + | これを解いて <math>\textstyle k = 1,\quad k = \frac{p}{1-p}</math>。このうち前者は ''p'' = 1/2 に対応するので除外します。境界条件<math>P(0) = 0\,</math>, <math>P(n) = 1\,</math>から <math>P(i) = a k^i+b\,</math> の係数 ''a'', ''b'' を求めると | ||
| + | <math>\textstyle | ||
| + | P(i) = \frac{k^i - 1}{k^n - 1} | ||
| + | </math> | ||
| + | |||
| + | となります。 | ||
| + | |||
| + | * ''p'' = 1/2 のとき <math>P(i) = i/n\,</math>。つまり勝率は開始時の所持金に正比例します。 | ||
| + | * ''p'' ≠ 1/2 のとき <math>\textstyle P(i) = \frac{k^i - 1}{k^n - 1}\ (k = \frac{p}{1-p})</math>。つまり勝率は ''k'' の値が 1 を少しでも上回れば 1 に大きく近づきます。 | ||
Revision as of 00:21, 7 July 2011
Contents |
反射壁と吸収壁
ここでは1次元のランダムウォークで、左右対称な場合 p = q = 1/2 を考えます。 ある位置 k* にきたら次のステップは確率 1 で k* - 1 に移動する場合、 k* を反射壁と呼びます。 反射壁があるときは、壁が無いとみなしてランダムウォークをしたあとに壁を折り返して一致する鏡像点の確率を足したものになります。 ウォーク後の位置を k とするとき、 k* の k に対する鏡像点は 2 k* - k なので、以下のようになります。
ある位置 k* にきたら次のステップ以降は移動できなくなる場合、 k* を吸収壁と呼びます。
吸収壁があるときは、壁がないとみなしてランダムウォークをしたあとに壁を折り返して一致する鏡像点の確率を引いたものになります。
- 壁がないとき、n ステップ後に位置 k に至る経路数は
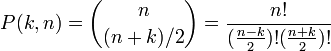
- 反射壁があるとき、n ステップ後に位置 k に至る経路数は
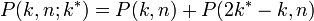
- 吸収壁があるとき、n ステップ後に位置 k に至る経路数は
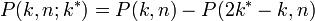
マイナスの値をとらない経路の数
マイナスの値をとらないことは、−1 の位置に吸収壁があることに相当します。たとえば 2 n ステップ後に原点に戻るウォークで 0 以上の部分だけを通る経路数は
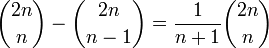
となり、カタラン数に一致します。
n ステップ後に初めて吸収壁 k に到達する経路の数
n ステップ後に k にいる経路の総数は 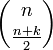 ですが、この中には k + 1 を経由するものが含まれます。
1 ステップ前の状態を考えると、位置は k - 1 か、k + 1 です。k + 1 に至る経路の総数は
ですが、この中には k + 1 を経由するものが含まれます。
1 ステップ前の状態を考えると、位置は k - 1 か、k + 1 です。k + 1 に至る経路の総数は 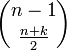 で、k - 1 に至る経路のうち反射壁を通るものの総数も鏡像の原理から
で、k - 1 に至る経路のうち反射壁を通るものの総数も鏡像の原理から 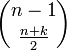 と等しくなります。
よって求める経路数は
と等しくなります。
よって求める経路数は
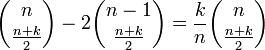
となります。つまり、初めて k に初めて到達する経路数は通常のランダムウォークを k/n 倍すればよいだけです。
ギャンブラーの破産問題
コインを i 枚持つギャンブラーが確率 p で表の出るコインを投げ、表がならコインを 1 枚受け取り、裏なら 1 枚失います。コインを全て失う前に n 枚に増える確率を考えましょう。
これは確率 p − 1, p で左右にそれぞれ 1 移動し、位置 0 と n を吸収壁とみなしたランダムウォークです。位置 0 が破産、位置 n を勝ちとみなして、位置 i における勝率を考えます。
勝率が満たす漸化式は

です。 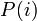 を求めましょう。
を求めましょう。
- p = 1/2 のとき
左右に公正に移動するウォークなので、漸化式を満たす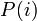 として等差数列
として等差数列 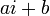 を仮定できます。境界条件
を仮定できます。境界条件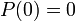 ,
, 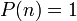 から
から 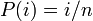 です。
です。
- p ≠ 1/2 のとき
左右に移動するたびに 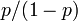 倍に勝率が変わるウォークなので、漸化式から
倍に勝率が変わるウォークなので、漸化式から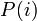 が等比数列
が等比数列 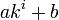 と予測できます。これを漸化式に代入しましょう。
と予測できます。これを漸化式に代入しましょう。
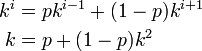
これを解いて  。このうち前者は p = 1/2 に対応するので除外します。境界条件
。このうち前者は p = 1/2 に対応するので除外します。境界条件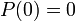 ,
, 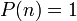 から
から 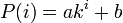 の係数 a, b を求めると
の係数 a, b を求めると
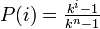
となります。
- p = 1/2 のとき
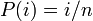 。つまり勝率は開始時の所持金に正比例します。
。つまり勝率は開始時の所持金に正比例します。
- p ≠ 1/2 のとき
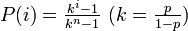 。つまり勝率は k の値が 1 を少しでも上回れば 1 に大きく近づきます。
。つまり勝率は k の値が 1 を少しでも上回れば 1 に大きく近づきます。