Aritalab:Lecture/NetworkBiology/Random Walk/Reflection

Revision as of 16:19, 4 July 2011

反射壁と吸収壁

ここでは1次元のランダムウォークで、左右対称な場合 p = q = 1/2 を考えます。ある位置 k^* にきたら次のステップは確率 1 で k^* - 1 に移動する場合、 k^* を反射壁と呼びます。反射壁があるときは、壁が無いとみなしてランダムウォークをしたあとに壁を折り返して一致する鏡像点の確率を足したものになります。ウォーク後の位置を k とするとき、 k^* の k に対する鏡像点は 2 k^* - k なので、以下のようになります。

ある位置 k^* にきたら次のステップ以降は移動できなくなる場合、 k^* を吸収壁と呼びます。吸収壁があるときは、壁がないとみなしてランダムウォークをしたあとに壁を折り返して一致する鏡像点の確率を引いたものになります。

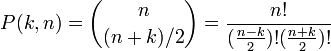
壁がないとき、n ステップ後に位置 k に至る経路数は $P(k,n) = \binom{n}{(n+k)/2} = \frac{n!}{(\frac{n - k}{2}) ! (\frac{n + k}{2}) !}$
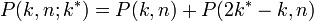
反射壁があるとき、n ステップ後に位置 k に至る経路数は $P(k, n; k^*) = P(k, n) + P(2k^* - k, n) \,$
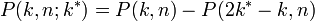
吸収壁があるとき、n ステップ後に位置 k に至る経路数は $P(k, n; k^*) = P(k, n) - P(2k^* - k, n) \,$

マイナスの値をとらない経路の数

マイナスの値をとらないことは、−1 の位置に吸収壁があることに相当します。たとえば 2 n ステップ後に原点に戻るウォークで 0 以上の部分だけを通る経路数は

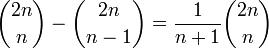
$\binom{2n}{n} - \binom{2n}{n-1} = \frac{1}{n+1} \binom{2n}{n}$

となり、カタラン数に一致します。

n ステップ後に初めて吸収壁 k に到達する経路の数

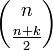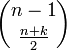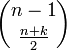n ステップ後に k にいる経路の総数は $\binom{n}{\frac{n+k}{2}}$ ですが、この中には k + 1 を経由するものが含まれます。 1 ステップ前の状態を考えると、位置は k - 1 か、k + 1 です。k + 1 に至る経路の総数は $\binom{n-1}{\frac{n+k}{2}}$ で、k - 1 に至る経路のうち反射壁を通るものの総数も鏡像の原理から $\binom{n-1}{\frac{n+k}{2}}$ と等しくなります。よって求める経路数は

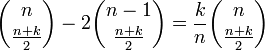
$\binom{n}{\frac{n+k}{2}} - 2 \binom{n-1}{\frac{n+k}{2}} = \frac{k}{n} \binom{n}{\frac{n+k}{2}}$

となります。つまり、初めて k に初めて到達する経路数は通常のランダムウォークを k/n 倍すればよいだけです。

ギャンブラーの破産問題

二人のプレーヤーがコインを k₁ と k₂ 枚ずつ持っています。確率 1/2 で勝てばコインを 1 枚うけとり、負ければ 1 枚渡します。勝負は原点から出発して左右に 1/2 の確率で移動するランダムウォークに相当し、時刻 t における位置はプレーヤー 1 が得たコインの枚数（勝ち数）です。状態 − k₁ になったらプレーヤー 1 が破産してゲームは終了し、k₂ になったらプレーヤー 2 が破産してゲームは終了します。このゲームは、状態 k₁ と k₂ が吸収壁とみなせます。

ゲームに勝つ確率

プレーヤー 1 が破産する前に k₂ 枚のコインを獲得する確率 q を求めましょう。

時刻 t において位置が i にいる確率を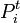 $P^t_{i}$ と書きましょう。すると

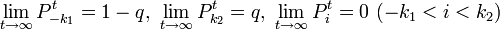
$\lim_{t\rightarrow \infty} P^t_{-k_1} = 1-q,\ \lim_{t\rightarrow \infty} P^t_{k_2} = q,\ \lim_{t\rightarrow \infty} P^t_{i} = 0 \ (-k_1 < i < k_2)$

となります。また、ゲームは公正なため、何回目の勝負であってもプレーヤー 1 が持つコイン数の期待値は 0 です。つまり時刻 t について数学的帰納法を用いると、常に

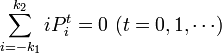
$\sum^{k_2}_{i = -k_1} i P^t_{i} = 0 \ (t = 0, 1, \cdots)$

です。極限を取ると

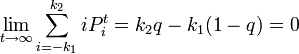
$\lim_{t\rightarrow \infty} \sum^{k_2}_{i = -k_1} i P^t_{i} = k_2 q - k_1 (1-q) = 0$

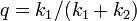となるので $\, q = k_1 / (k_1 + k_2)$ です。つまりゲームに勝つ確率は、開始時の持ち点に比例します。つまり、公正なコインを用いた賭けでさえ、資金が少ないギャンブラーが資金の多い胴元に勝つ見込みは少なくなります。

@@ Line 39: / Line 39: @@
 ==ギャンブラーの破産問題==
-二人のプレーヤーがコインを ''k''<sub>1</sub> と ''k''<sub>2</sub> 枚ずつ持っています。確率 1/2 で勝てばコインを 1 枚うけとり、負ければ 1 枚渡します。勝負は原点から出発して左右に 1/2 の確率で移動するランダムウォークに相当し、時刻 ''t'' における位置はプレーヤー 1 が得たコインの枚数（勝ち数）です。状態 &minus; ''k''<sub>1</sub> になったらプレーヤー 1 が破産してゲームは終了し、''k''<sub>2</sub> になったらプレーヤー 2 が破産してゲームは終了します。このゲームは、状態 ''k''<sub>1</sub> と ''k''<sub>2</sub> が吸収壁とみなせます。プレーヤー 1 が破産する前に ''k''<sub>2</sub> 枚のコインを獲得する確率 ''q'' を求めましょう。
+二人のプレーヤーがコインを ''k''<sub>1</sub> と ''k''<sub>2</sub> 枚ずつ持っています。確率 1/2 で勝てばコインを 1 枚うけとり、負ければ 1 枚渡します。勝負は原点から出発して左右に 1/2 の確率で移動するランダムウォークに相当し、時刻 ''t'' における位置はプレーヤー 1 が得たコインの枚数（勝ち数）です。状態 &minus; ''k''<sub>1</sub> になったらプレーヤー 1 が破産してゲームは終了し、''k''<sub>2</sub> になったらプレーヤー 2 が破産してゲームは終了します。このゲームは、状態 ''k''<sub>1</sub> と ''k''<sub>2</sub> が吸収壁とみなせます。
+===ゲームに勝つ確率===
+プレーヤー 1 が破産する前に ''k''<sub>2</sub> 枚のコインを獲得する確率 ''q'' を求めましょう。
 時刻 ''t'' において位置が ''i'' にいる確率を<math>P^t_{i}</math> と書きましょう。すると
@@ Line 54: / Line 57: @@
 となるので <math>\, q = k_1 / (k_1 + k_2) </math> です。つまりゲームに勝つ確率は、開始時の持ち点に比例します。
+つまり、公正なコインを用いた賭けでさえ、資金が少ないギャンブラーが資金の多い胴元に勝つ見込みは少なくなります。
-;考察
-: 公正なコインを用いた賭けでも、資金が少ないギャンブラーが資金の多い胴元に勝つ見込みは少ない。

Aritalab:Lecture/NetworkBiology/Random Walk/Reflection

Revision as of 16:19, 4 July 2011

Contents

反射壁と吸収壁

マイナスの値をとらない経路の数

n ステップ後に初めて吸収壁 k に到達する経路の数

ギャンブラーの破産問題

ゲームに勝つ確率

Personal tools

Namespaces

Variants

Views

Actions

Search

Navigation

metabolites

Toolbox