Aritalab:Lecture/NetworkBiology/Barabasi-Albert Model
m |
m |
||
| (18 intermediate revisions by one user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | __TOC__ | |
| − | == | + | ==スケールフリー性== |
| − | + | ||
| − | + | 多くの研究論文で「スケールフリー」という言葉が使われます。もともとは「桁 (scale) に依存しない (free) 性質」を意味し、昔から物理学の世界で知られていたものです。日本語ではべき則と呼ばれます。ただし、ネットワークについては1999年から言われはじめました。ネットワークの頂点に接続する辺の数を次数といい、全頂点のなかで次数 ''k'' の頂点の占める割合を p(k) と書きます。ネットワークがスケールフリーであるとは次数の分布がべき則に従うことを意味し、式で書くと p(k) ∝ k<sup>-λ</sup> になります。 | |
| − | + | ||
| − | になります。 | + | |
この定義は1999年の論文 Barabási A-L, Albert R "Emergence of Scaling in Random Networks" [http://www.sciencemag.org/content/286/5439/509.abstract ''Science'' 286(5439):509-512] をきっかけに広まりました。 | この定義は1999年の論文 Barabási A-L, Albert R "Emergence of Scaling in Random Networks" [http://www.sciencemag.org/content/286/5439/509.abstract ''Science'' 286(5439):509-512] をきっかけに広まりました。 | ||
| − | + | 自然界にはべき則が普通にみられ、以下の例がよく知られています。(この表におけるL, Cの意味は[[Aritalab:Lecture/NetworkBiology/Link_Analysis|リンク解析]]の項を参照。) | |
{| class="wikitable" | {| class="wikitable" | ||
| − | ! Network (size) || | + | ! Network (size) || λ || ''L'' || ''C'' || |
|- | |- | ||
| − | | インターネット (1.5 x 10<sup>5</sup>) || < | + | | インターネット (1.5 x 10<sup>5</sup>) || λ<sub>in</sub>=2.1, λ<sub>out</sub>=2.7 || 3.1 || 0.11 || Barabasi and Albert (1999) |
|- | |- | ||
| 部分的インターネット (3000-6000) || 2.16 || 3.7 || 0.18-0.3 || Faloutous et al. (1999) | | 部分的インターネット (3000-6000) || 2.16 || 3.7 || 0.18-0.3 || Faloutous et al. (1999) | ||
| Line 23: | Line 21: | ||
|} | |} | ||
| − | + | しかし、べき則やそれを生み出すメカニズムは最近わかった事実ではありません。科学界ではおよそ50年周期で話題になってきました。べき則を示す有名な例として、[http://www.nslij-genetics.org/wli/zipf/ ジップの法則]、パレートの法則などがあります。 | |
* 20世紀初頭 | * 20世紀初頭 | ||
** Pareto, V. (1896, 1897) Cours d’economie politique. Reprinted as a volume of Oeuvres Complètes (Droz, Geneva, 1896, 1965). Pareto, V. Cours d’Economique Politique (Macmillan, Paris, 1897) 所得の分布がべき則に従うことを示す | ** Pareto, V. (1896, 1897) Cours d’economie politique. Reprinted as a volume of Oeuvres Complètes (Droz, Geneva, 1896, 1965). Pareto, V. Cours d’Economique Politique (Macmillan, Paris, 1897) 所得の分布がべき則に従うことを示す | ||
| − | ** Yule, G. (1924) A mathematical theory of evolution, based on the conclusion of Dr. J.C. Willis. F.R.S. Phil. Trans. R. Soc. Lond Ser. B 213, 21–87 優先的選択のメカニズムを示す | + | ** Yule, G. (1924) A mathematical theory of evolution, based on the conclusion of Dr. J.C. Willis. ''F.R.S. Phil. Trans. R. Soc. Lond Ser. B'' 213, 21–87 優先的選択のメカニズムを示す |
* 20世紀半ば | * 20世紀半ば | ||
** Zipf, G.K. (1949) Human Behavior and the Principle of Least Effort, Addison-Wesley 単語の頻度分布がべき則に従うことを示す | ** Zipf, G.K. (1949) Human Behavior and the Principle of Least Effort, Addison-Wesley 単語の頻度分布がべき則に従うことを示す | ||
| − | ** Simon, H.A. (1955) On a class of skew distribution functions. Biometrika 42, 425–440 乗算過程が漸近的にべき則に従うことを示す | + | ** Simon, H.A. (1955) On a class of skew distribution functions. ''Biometrika'' 42, 425–440 乗算過程が漸近的にべき則に従うことを示す |
* 21世紀初頭 | * 21世紀初頭 | ||
** Barabási A-L, Albert R (1999) これまでの研究をネットワークの言葉に置き換える | ** Barabási A-L, Albert R (1999) これまでの研究をネットワークの言葉に置き換える | ||
またべき則に近い形である対数正規分布とべき則の関係についても多くの研究がなされました。 | またべき則に近い形である対数正規分布とべき則の関係についても多くの研究がなされました。 | ||
| − | * | + | * 乗算過程による対数正規分布の一般性(20世紀初頭) |
| − | ** Kapteyn, J.C. (1903) Skew frequency curves in biology and statistics in Astronomical Laboratory, Noordhoff, Groningen | + | ** Kapteyn, J.C. (1903) Skew frequency curves in biology and statistics in Astronomical Laboratory, Noordhoff, Groningen |
| − | ** Gibrat, R. (1931) Les Inegalites Economiques, Libraire du Recueil Sirey, Paris | + | :: 様々な事象が対数正規分布をなすことを示した論文 |
| − | * | + | ** Gibrat, R. (1931) Les Inegalites Economiques, ''Libraire du Recueil Sirey, Paris'' |
| − | ** Kesten, H. (1973) Random difference equations and renewal theory for products of random matrices. Acta Mathematica CXXXI, 207–248 | + | :: 企業サイズが対数正規分布をなすことを示した論文。その後、都市のサイズ等が対数正規分布に従うことが Gibrat's law と呼ばれる。ただ、都市サイズが power law (zipf's law) に従うとする論文もある。(英語版ウィキペディア [https://en.wikipedia.org/wiki/Gibrat%27s_law Gibrat's law]) |
| − | ** Reed, W.J. and Hughes, B.D. (2002) From gene families and genera to incomes and internet file sizes: why power-laws are so common in nature. Phys. Rev. E 66, 067103 | + | |
| + | * 乗算過程がべき則を生むメカニズム(20世紀半ば) | ||
| + | ** Kesten, H. (1973) Random difference equations and renewal theory for products of random matrices. ''Acta Mathematica CXXXI'', 207–248 | ||
| + | :: 対数正規分布をつくるランダムウォークでサイズが小さい部分に反射壁があるとべき分布になることを数理的に示した論文 | ||
| + | * 最近 (21世紀初頭) | ||
| + | ** Reed, W.J. and Hughes, B.D. (2002) From gene families and genera to incomes and internet file sizes: why power-laws are so common in nature. ''Phys. Rev. E'' 66, 067103 | ||
| + | |||
| + | バラバシの論文やレビューにはネットワークのスケールフリー性を自分たちがあたかも初めて見つけたかのように書いていますが、その姿勢が不誠実であることは筆者を含む複数の論文が指摘しています。 | ||
| + | |||
| + | * Arita, M. (2005 Jul.) Scale-freeness and biological networks. ''J Biochem.'' 138(1):1-4. | ||
| + | * Keller, EF. (2005 Oct.) Revisiting "scale-free" networks. ''Bioessays'' 27(10):1060-8. | ||
==Barabási-Albert Model== | ==Barabási-Albert Model== | ||
Barabási, Albertがネットワークの成長モデルとして提唱したのは以下の過程です。(正確には初期条件が異なるが本質は同じ。) | Barabási, Albertがネットワークの成長モデルとして提唱したのは以下の過程です。(正確には初期条件が異なるが本質は同じ。) | ||
| − | # | + | # 時間ステップ 0 における 1 頂点からスタートする。 |
# 単位時間毎に頂点を1つずつ追加し、既に存在する頂点と<math>m</math>本の辺でつなぐ。<br/>新しい辺はそれぞれ確率<math>\textstyle p_i = k_i / \sum_j k_j</math> (ここで<math>k_i</math>は頂点''i''の次数) で接続先を決定する。 | # 単位時間毎に頂点を1つずつ追加し、既に存在する頂点と<math>m</math>本の辺でつなぐ。<br/>新しい辺はそれぞれ確率<math>\textstyle p_i = k_i / \sum_j k_j</math> (ここで<math>k_i</math>は頂点''i''の次数) で接続先を決定する。 | ||
この過程は優先的選択(preferential attachment)と呼ばれ、一般に''rich gets richer''メカニズムなどともいわれます。 | この過程は優先的選択(preferential attachment)と呼ばれ、一般に''rich gets richer''メカニズムなどともいわれます。 | ||
| − | + | ==べき則のパラメータ<math>\lambda</math> (ラムダ) について== | |
| − | ==べき則のパラメータ<math>\ | + | BAモデルから<math>\lambda = 3 </math>を簡単に導出できます。 |
| − | BAモデルから<math>\ | + | 初期条件として時刻 0 に 1 頂点の場合、<math>t</math>時間後には頂点数<math>t+1</math>、辺数 <math>mt</math> です。 |
| − | + | ||
頂点 ''i'' の次数 <math>k_i</math> は時間が経つと単調増加します。ここで、次数を <math>k_i(t)</math> という連続関数として考えてみます。頂点 ''i'' の次数は単位時間あたり次数 <math>k_i</math> に比例して増加するので | 頂点 ''i'' の次数 <math>k_i</math> は時間が経つと単調増加します。ここで、次数を <math>k_i(t)</math> という連続関数として考えてみます。頂点 ''i'' の次数は単位時間あたり次数 <math>k_i</math> に比例して増加するので | ||
<center> | <center> | ||
| Line 59: | Line 66: | ||
これを解くと <math>\textstyle k_i(t) = m(t/t_i)^{1/2}</math>、 | これを解くと <math>\textstyle k_i(t) = m(t/t_i)^{1/2}</math>、 | ||
ただし <math>t_i</math> は頂点 <math>i</math> が追加された時間で <math>k_i(t_i)=m</math> となる値です(初期条件)。 | ただし <math>t_i</math> は頂点 <math>i</math> が追加された時間で <math>k_i(t_i)=m</math> となる値です(初期条件)。 | ||
| − | これを式変形すれば、頂点の次数がある値 <math> | + | これを式変形すれば、頂点の次数がある値 <math>k</math> になる時間は <math>t=t_i(k/m)^2\,</math> であることがわかります。 |
| + | 頂点 <math>i</math> の次数(期待値)が <math>k</math> のとき、<math>t_i</math> 以前に追加された頂点の次数は全て <math>k</math> 以上になっています。 | ||
| − | 頂点の次数分布 ''p(k)'' を求めるために、まず頂点の次数が <math>k</math> より大きくなる割合(累積分布関数)を求めます。次数が '' | + | |
| + | 頂点の次数分布 ''p(k)'' を求めるために、まず頂点の次数が <math>k</math> より大きくなる割合(累積分布関数)を求めます。次数が ''k'' より大きくなるような頂点全体の割合は、時刻 <math>t(m/k)^2\,</math> より前に追加された頂点全体の割合に等しくなります。 | ||
<center> | <center> | ||
| − | <math>Pr | + | <math>\mbox{Pr}[k_i(t) > k] |
| + | = \mbox{Pr}[t_i < t(\frac{m}{k})^2] | ||
| + | = (\frac{m}{k})^2</math> | ||
</center> | </center> | ||
| − | 左の等号は、頂点 <math>i</math> が追加された時間 <math>t_i</math> が、時刻 <math>t</math> に対して <math>(m/k)^2</math> よりも早ければ(小さければ)、次数が <math> | + | 左の等号は、頂点 <math>i</math> が追加された時間 <math>t_i</math> が、時刻 <math>t</math> に対して <math>(m/k)^2\,</math> よりも早ければ(小さければ)、次数が <math>k</math> を超えることを示しています。 |
| − | 頂点が常に一定量ずつ追加されることを考えると、全体サイズを1とするなら、その割合は単純に <math>( | + | 頂点が常に一定量ずつ追加されることを考えると、全体サイズを1とするなら、その割合は単純に <math>(m/k)^2\,</math> としてよいことがわかります。 |
| − | 次数分布 <math>Pr | + | 次数分布 <math>\mbox{Pr}[k_i(t) = k]\,</math> は <math>\mbox{Pr}[k_i(t) > k] - \mbox{Pr}[k_i(t) > k+1]\,</math> と書けるので、その差は''k''を変数と考えて <math>\textstyle - \frac{d}{d k}\mbox{Pr}[k_i(t) > k]</math> になります。 |
| − | + | 実際に<math>k</math>で微分すると<math>\mbox{Pr}[k_i(t) = k] = \frac{2m^2}{k^3}</math>。すなわち辺の次数は<math>k^{-3}</math>に比例します。 | |
| − | + | ==優先的選択でない場合== | |
| − | + | 新しい辺が結びつく先が次数に比例する値ではなく、一様分布に従うと仮定してみます。頂点 ''i'' は頂点数に正比例して辺を得る確率が減っていきます。 | |
<center> | <center> | ||
<math>\frac{\partial k_i}{\partial t} = m/(n-1) = m/t</math> | <math>\frac{\partial k_i}{\partial t} = m/(n-1) = m/t</math> | ||
</center> | </center> | ||
| − | + | これを解くと <math> k_i(t) = m \log t + const. </math> です。 | |
| + | 初期条件として 頂点 ''i'' が追加された時間 <math>t_i</math> に辺の数が ''m'' であること <math>k_i(t_i) = m</math> をいれると <math>k_i(t) = m\Big(\log(\frac{t}{t_i})+1\Big)</math>。頂点 ''i'' の次数が ''k'' になる時間は <math>k_i \exp(k/m -1)</math> であることがわかります。 | ||
| + | こちらも累積分布関数を計算してみましょう。 | ||
<center> | <center> | ||
| − | <math> | + | <math>\mbox{Pr}[k_i(t) > k] = \mbox{Pr}\Big[t_i < t\Big(\frac{1}{\exp(k/m - 1)}\Big)\Big] = ee^{-k/m}</math> |
</center> | </center> | ||
| − | + | これを上のセクションと同様に微分することで<math>\mbox{Pr}[k_i(t)=k] = \frac{e}{m}e^{-k/m}</math>、すなわち辺の次数は指数的に減少することになります。 | |
| + | |||
| + | ==何がべき分布を作るのか== | ||
| + | バラバシ-アルバートモデルについて言われる批判のひとつに、自然界においてはべき則のパラメータλの多くが2から3の間をとるのにλ=3のときしか説明できないというものがあります。これはどちらかというと的を外した意見です。 | ||
| − | + | べき則のパラメータが定数になる理由のエッセンスは、優先的選択において次数の時間変化を規定する微分方程式が <math>\textstyle \frac{dy}{dx} = \frac{y}{2x}</math> つまり <math>y/x</math> の形をとることです。この方程式を解くと<math>y=cx^{1/2}</math>という答えが得られ(<math>c</math>は適当な定数)、この係数1/2が<math>\lambda=-3</math>を作り出します。だから異なる<math>\lambda</math>の値を作り出すには<math>y/2x</math>における比の2を他にずらせばよいのです。 | |
| − | + | ||
| − | <math>\textstyle \frac{dy}{dx} = \frac{y}{2x}</math> | + | |
| − | |||
<center> | <center> | ||
<math>\frac{\partial k_i}{\partial t} = \frac{k_i}{pt}</math> | <math>\frac{\partial k_i}{\partial t} = \frac{k_i}{pt}</math> | ||
</center> | </center> | ||
| − | + | という近似を何らかの形で導出できれば、<math>\lambda=p+1</math>になります。 | |
<!---- | <!---- | ||
==適応度モデル== | ==適応度モデル== | ||
| − | 各頂点<math>i</math>が「適応度」<math>\eta_i</math>を持ち、優先的選択の確率を<math>\textstyle p = \eta_i k_i/\sum_j \eta_jk_j</math>で表すバリエーション(Bianconi G and Barabasi AL 2001)。BAモデルのパラメータ<math>\ | + | 各頂点<math>i</math>が「適応度」<math>\eta_i</math>を持ち、優先的選択の確率を<math>\textstyle p = \eta_i k_i/\sum_j \eta_jk_j</math>で表すバリエーション(Bianconi G and Barabasi AL 2001)。BAモデルのパラメータ<math>\lambda=-3</math>は<math>k_i(t) = f(t)</math>と表現した際の<math>t</math>の係数<math>1/2</math>より導出される。適応度を導入して<math>\partial k_i/\partial t</math>の比を<math>k_i/2t</math>からずらすことができればよい。そこで<math>\eta_i</math>を適当に近似することで(例えば<math>2k_i/3t</math>をつくる)、<math>\lambda=-3</math>以外を導出できる。 |
==頂点非活性化モデル== | ==頂点非活性化モデル== | ||
頂点を一つ追加するたびに現存する頂点のいずれか一つをランダムに非活性化し、いったん非活性になると辺を受け取らなくなるバリエーション (Klemm K and Eguiluz VM 2002)を考えよう。(活性状態の頂点は常に一定数である点に注意。)次数<math>k</math>で生き残る頂点の割合を<math>1-P(k)</math>で表現すると、十分大きい<math>t\simeq \infty</math>の定常状態において<math>p^{\infty}(k+1) = (1-P(k)) p^{\infty}(k)</math>が成立する。ここで<math>k</math>を連続値に読み替えると | 頂点を一つ追加するたびに現存する頂点のいずれか一つをランダムに非活性化し、いったん非活性になると辺を受け取らなくなるバリエーション (Klemm K and Eguiluz VM 2002)を考えよう。(活性状態の頂点は常に一定数である点に注意。)次数<math>k</math>で生き残る頂点の割合を<math>1-P(k)</math>で表現すると、十分大きい<math>t\simeq \infty</math>の定常状態において<math>p^{\infty}(k+1) = (1-P(k)) p^{\infty}(k)</math>が成立する。ここで<math>k</math>を連続値に読み替えると | ||
| − | <math>\textstyle p^{\infty}(k+1) -p^{\infty}(k)= \frac{\partial p^{\infty}(k)}{\partial k} = -P(k) p^{\infty}(k) </math>を導ける。ここで<math>P(k)</math>の式として、非活性化する頂点は次数の逆数に比例する優先的選択に従うと仮定する。つまり次数が大きい頂点ほど生き残りやすいという名目で<math>P(k)=c/k</math>にすると、パラメータ<math>c</math>を適当に調節することで容易に<math>\ | + | <math>\textstyle p^{\infty}(k+1) -p^{\infty}(k)= \frac{\partial p^{\infty}(k)}{\partial k} = -P(k) p^{\infty}(k) </math>を導ける。ここで<math>P(k)</math>の式として、非活性化する頂点は次数の逆数に比例する優先的選択に従うと仮定する。つまり次数が大きい頂点ほど生き残りやすいという名目で<math>P(k)=c/k</math>にすると、パラメータ<math>c</math>を適当に調節することで容易に<math>\lambda=3</math>以外を作り出せる。 |
Latest revision as of 09:03, 2 August 2017
Contents |
[edit] スケールフリー性
多くの研究論文で「スケールフリー」という言葉が使われます。もともとは「桁 (scale) に依存しない (free) 性質」を意味し、昔から物理学の世界で知られていたものです。日本語ではべき則と呼ばれます。ただし、ネットワークについては1999年から言われはじめました。ネットワークの頂点に接続する辺の数を次数といい、全頂点のなかで次数 k の頂点の占める割合を p(k) と書きます。ネットワークがスケールフリーであるとは次数の分布がべき則に従うことを意味し、式で書くと p(k) ∝ k-λ になります。
この定義は1999年の論文 Barabási A-L, Albert R "Emergence of Scaling in Random Networks" Science 286(5439):509-512 をきっかけに広まりました。
自然界にはべき則が普通にみられ、以下の例がよく知られています。(この表におけるL, Cの意味はリンク解析の項を参照。)
| Network (size) | λ | L | C | |
|---|---|---|---|---|
| インターネット (1.5 x 105) | λin=2.1, λout=2.7 | 3.1 | 0.11 | Barabasi and Albert (1999) |
| 部分的インターネット (3000-6000) | 2.16 | 3.7 | 0.18-0.3 | Faloutous et al. (1999) |
| 映画俳優の共演関係 (2.2 x 105) | 2.3 | 3.7 | 0.79 | Watts and Strogatz (1998) |
| PubMedデータベースの共著関係 (1.5 x 106) | ? | 4.6 | 0.066 | Newman (2000, 2001) |
しかし、べき則やそれを生み出すメカニズムは最近わかった事実ではありません。科学界ではおよそ50年周期で話題になってきました。べき則を示す有名な例として、ジップの法則、パレートの法則などがあります。
- 20世紀初頭
- Pareto, V. (1896, 1897) Cours d’economie politique. Reprinted as a volume of Oeuvres Complètes (Droz, Geneva, 1896, 1965). Pareto, V. Cours d’Economique Politique (Macmillan, Paris, 1897) 所得の分布がべき則に従うことを示す
- Yule, G. (1924) A mathematical theory of evolution, based on the conclusion of Dr. J.C. Willis. F.R.S. Phil. Trans. R. Soc. Lond Ser. B 213, 21–87 優先的選択のメカニズムを示す
- 20世紀半ば
- Zipf, G.K. (1949) Human Behavior and the Principle of Least Effort, Addison-Wesley 単語の頻度分布がべき則に従うことを示す
- Simon, H.A. (1955) On a class of skew distribution functions. Biometrika 42, 425–440 乗算過程が漸近的にべき則に従うことを示す
- 21世紀初頭
- Barabási A-L, Albert R (1999) これまでの研究をネットワークの言葉に置き換える
またべき則に近い形である対数正規分布とべき則の関係についても多くの研究がなされました。
- 乗算過程による対数正規分布の一般性(20世紀初頭)
- Kapteyn, J.C. (1903) Skew frequency curves in biology and statistics in Astronomical Laboratory, Noordhoff, Groningen
- 様々な事象が対数正規分布をなすことを示した論文
- Gibrat, R. (1931) Les Inegalites Economiques, Libraire du Recueil Sirey, Paris
- 企業サイズが対数正規分布をなすことを示した論文。その後、都市のサイズ等が対数正規分布に従うことが Gibrat's law と呼ばれる。ただ、都市サイズが power law (zipf's law) に従うとする論文もある。(英語版ウィキペディア Gibrat's law)
- 乗算過程がべき則を生むメカニズム(20世紀半ば)
- Kesten, H. (1973) Random difference equations and renewal theory for products of random matrices. Acta Mathematica CXXXI, 207–248
- 対数正規分布をつくるランダムウォークでサイズが小さい部分に反射壁があるとべき分布になることを数理的に示した論文
- 最近 (21世紀初頭)
- Reed, W.J. and Hughes, B.D. (2002) From gene families and genera to incomes and internet file sizes: why power-laws are so common in nature. Phys. Rev. E 66, 067103
バラバシの論文やレビューにはネットワークのスケールフリー性を自分たちがあたかも初めて見つけたかのように書いていますが、その姿勢が不誠実であることは筆者を含む複数の論文が指摘しています。
- Arita, M. (2005 Jul.) Scale-freeness and biological networks. J Biochem. 138(1):1-4.
- Keller, EF. (2005 Oct.) Revisiting "scale-free" networks. Bioessays 27(10):1060-8.
[edit] Barabási-Albert Model
Barabási, Albertがネットワークの成長モデルとして提唱したのは以下の過程です。(正確には初期条件が異なるが本質は同じ。)
- 時間ステップ 0 における 1 頂点からスタートする。
- 単位時間毎に頂点を1つずつ追加し、既に存在する頂点と
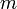 本の辺でつなぐ。
本の辺でつなぐ。
新しい辺はそれぞれ確率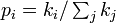 (ここで
(ここで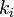 は頂点iの次数) で接続先を決定する。
は頂点iの次数) で接続先を決定する。
この過程は優先的選択(preferential attachment)と呼ばれ、一般にrich gets richerメカニズムなどともいわれます。
[edit] べき則のパラメータ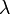 (ラムダ) について
(ラムダ) について
BAモデルから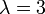 を簡単に導出できます。
初期条件として時刻 0 に 1 頂点の場合、
を簡単に導出できます。
初期条件として時刻 0 に 1 頂点の場合、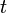 時間後には頂点数
時間後には頂点数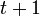 、辺数
、辺数 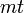 です。
頂点 i の次数
です。
頂点 i の次数 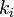 は時間が経つと単調増加します。ここで、次数を
は時間が経つと単調増加します。ここで、次数を 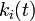 という連続関数として考えてみます。頂点 i の次数は単位時間あたり次数
という連続関数として考えてみます。頂点 i の次数は単位時間あたり次数 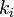 に比例して増加するので
に比例して増加するので
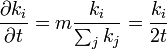
これを解くと 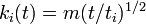 、
ただし
、
ただし 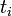 は頂点
は頂点 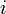 が追加された時間で
が追加された時間で 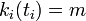 となる値です(初期条件)。
これを式変形すれば、頂点の次数がある値
となる値です(初期条件)。
これを式変形すれば、頂点の次数がある値 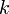 になる時間は
になる時間は 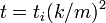 であることがわかります。
頂点
であることがわかります。
頂点 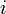 の次数(期待値)が
の次数(期待値)が 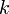 のとき、
のとき、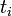 以前に追加された頂点の次数は全て
以前に追加された頂点の次数は全て 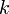 以上になっています。
以上になっています。
頂点の次数分布 p(k) を求めるために、まず頂点の次数が 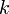 より大きくなる割合(累積分布関数)を求めます。次数が k より大きくなるような頂点全体の割合は、時刻
より大きくなる割合(累積分布関数)を求めます。次数が k より大きくなるような頂点全体の割合は、時刻 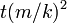 より前に追加された頂点全体の割合に等しくなります。
より前に追加された頂点全体の割合に等しくなります。
![\mbox{Pr}[k_i(t) > k]
= \mbox{Pr}[t_i < t(\frac{m}{k})^2]
= (\frac{m}{k})^2](/mediawiki/images/math/9/7/5/975ec0001115541e034a1203cc0f4e4c.png)
左の等号は、頂点 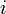 が追加された時間
が追加された時間 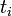 が、時刻
が、時刻 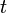 に対して
に対して 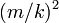 よりも早ければ(小さければ)、次数が
よりも早ければ(小さければ)、次数が 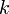 を超えることを示しています。
頂点が常に一定量ずつ追加されることを考えると、全体サイズを1とするなら、その割合は単純に
を超えることを示しています。
頂点が常に一定量ずつ追加されることを考えると、全体サイズを1とするなら、その割合は単純に 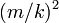 としてよいことがわかります。
としてよいことがわかります。
次数分布 ![\mbox{Pr}[k_i(t) = k]\,](/mediawiki/images/math/8/6/1/861b94d8d0e2e3d78b37abddd7d80045.png) は
は ![\mbox{Pr}[k_i(t) > k] - \mbox{Pr}[k_i(t) > k+1]\,](/mediawiki/images/math/e/2/0/e204fe0c4634a882dd46b6183a15c3a7.png) と書けるので、その差はkを変数と考えて
と書けるので、その差はkを変数と考えて ![\textstyle - \frac{d}{d k}\mbox{Pr}[k_i(t) > k]](/mediawiki/images/math/3/6/f/36fc39a8a8534d88b4d807df0a9b2621.png) になります。
実際に
になります。
実際に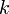 で微分すると
で微分すると![\mbox{Pr}[k_i(t) = k] = \frac{2m^2}{k^3}](/mediawiki/images/math/5/2/0/5208e3f5a0a546de1e7a079a513cda7b.png) 。すなわち辺の次数は
。すなわち辺の次数は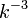 に比例します。
に比例します。
[edit] 優先的選択でない場合
新しい辺が結びつく先が次数に比例する値ではなく、一様分布に従うと仮定してみます。頂点 i は頂点数に正比例して辺を得る確率が減っていきます。
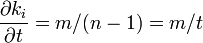
これを解くと 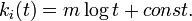 です。
初期条件として 頂点 i が追加された時間
です。
初期条件として 頂点 i が追加された時間 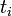 に辺の数が m であること
に辺の数が m であること 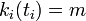 をいれると
をいれると 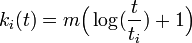 。頂点 i の次数が k になる時間は
。頂点 i の次数が k になる時間は 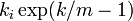 であることがわかります。
こちらも累積分布関数を計算してみましょう。
であることがわかります。
こちらも累積分布関数を計算してみましょう。
![\mbox{Pr}[k_i(t) > k] = \mbox{Pr}\Big[t_i < t\Big(\frac{1}{\exp(k/m - 1)}\Big)\Big] = ee^{-k/m}](/mediawiki/images/math/3/5/9/3591adeb9070bf312b7a84573e0749fc.png)
これを上のセクションと同様に微分することで![\mbox{Pr}[k_i(t)=k] = \frac{e}{m}e^{-k/m}](/mediawiki/images/math/5/e/a/5ea8baa6d4036bc354c5a48938aa9319.png) 、すなわち辺の次数は指数的に減少することになります。
、すなわち辺の次数は指数的に減少することになります。
[edit] 何がべき分布を作るのか
バラバシ-アルバートモデルについて言われる批判のひとつに、自然界においてはべき則のパラメータλの多くが2から3の間をとるのにλ=3のときしか説明できないというものがあります。これはどちらかというと的を外した意見です。
べき則のパラメータが定数になる理由のエッセンスは、優先的選択において次数の時間変化を規定する微分方程式が  つまり
つまり 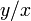 の形をとることです。この方程式を解くと
の形をとることです。この方程式を解くと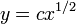 という答えが得られ(
という答えが得られ( は適当な定数)、この係数1/2が
は適当な定数)、この係数1/2が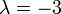 を作り出します。だから異なる
を作り出します。だから異なる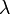 の値を作り出すには
の値を作り出すには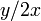 における比の2を他にずらせばよいのです。
における比の2を他にずらせばよいのです。

という近似を何らかの形で導出できれば、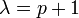 になります。
になります。