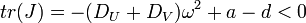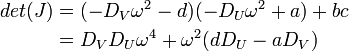Aritalab:Lecture/Bioinformatics/Turing
(Created page with "==拡散==拡散現象== 左右に等確率で移動する一次元のランダムウォークを考えます。原点から出発し、時間ステップ n における粒...") |
m |
||
| Line 1: | Line 1: | ||
| − | + | ==拡散現象== | |
左右に等確率で移動する一次元のランダムウォークを考えます。原点から出発し、時間ステップ n における粒子 x の位置を x(n) と記します。 | 左右に等確率で移動する一次元のランダムウォークを考えます。原点から出発し、時間ステップ n における粒子 x の位置を x(n) と記します。 | ||
Latest revision as of 06:23, 23 April 2013
Contents |
[edit] 拡散現象
左右に等確率で移動する一次元のランダムウォークを考えます。原点から出発し、時間ステップ n における粒子 x の位置を x(n) と記します。
です。粒子数を N として n ステップ後の位置の期待値と分散を計算します。
ここで連続値である時間変数を 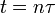 、拡散定数
、拡散定数 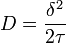 とおきます。すると
とおきます。すると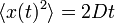 です。粒子は時間の平方根に比例する値で広がっていきます。
です。粒子は時間の平方根に比例する値で広がっていきます。
次に、一列に並んだ N 個の箱を考え、i 番目の箱の粒子密度を ui(t) とします。各粒子は時間ステップ毎に左右の箱にランダムウォークをすると考えます。単位時間あたり k の割合で箱の左右に移動するとき
つまり左右の箱の中にある粒子数との差を測って平均化する方向に変化しているはずです。
流れは密度の勾配に正比例すると考え、平均化のために移動する正味の粒子数をフラックス J と書くと、ある領域で粒子数が増加する方向を正として測った式は 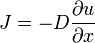 になります。
さて、区間 [ a , b ] における粒子の出入りは b から出る量と a から入る量を足しあわせればよく
になります。
さて、区間 [ a , b ] における粒子の出入りは b から出る量と a から入る量を足しあわせればよく
すなわち任意の区間で 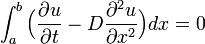 となるので
となるので
これを多次元に拡張した式が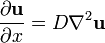 です。
です。
[edit] フィッシャー方程式
ロジスティック方程式に従う生物の個体群が、拡散方程式に従ってある領域に広がるモデルを、提案者 Sir Ronald Fisher にちなんでフィッシャー方程式と呼びます(統計学で有名な人です)。
境界条件として外には出られないことにします。
自明な解は U = 0, U = 1 の2つあります。その挙動は直感的にもすぐわかります。 U = 0 の周りは dU/dt > 0 なので不安定で U は増加し、U = 1 の周りは安定で 1 に収束します。 空間を考慮する場合、原点において U(0,0) = 1 の初期値が時間とともに(同心円上に)進行波を描きます。 このモデルは生物の分布域拡大を表現することが知られています。[1]
[edit] チューリングモデル
計算機科学の祖であるアラン・チューリング (Alan Turing) はパターン生成原理の提唱者としても知られています。
活性化因子 U と抑制因子 V の2成分からなる線形微分方程式を考えます。
活性化因子は自分と抑制因子をともに活性化しますが、抑制因子は両者を抑制します。 ヤコビ行列を J とすると tr(J) = a - d, det(J) = -ad + bc となり 原点の周りで安定になる条件 det(J) > 0 つまり bc > ad と、tr(J) < 0 つまり a < d となります。[2] 直感的には、U , V が大きくならなければ 0 に留まるので a や d というパラメータが小さく、活性化因子の勢いが少ない方が安定するとわかります。この二因子が空間内で相互作用する場合を考えましょう。
一次元空間を表すパラメータを x とし、拡散項 DU, DV を導入します。
定常解は時間異存項と場所異存項の積で表現できると仮定しましょう。
再びヤコビ行列 J を考えます。 安定条件の1つ
は、d > a の時なら成立します(拡散項が無い場合に同じ)。これは空間を考慮しなかった時に同じです。拡散係数の分、安定しやすくもなっています。 もう一つの条件は空間を考慮しなかった場合より不安定化しやすくなっています。不安定化の瀬戸際である ad = bc と仮定してみます。
これより d > a だとしても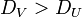 であれば det(J)が負になり得ることがわかります。このように拡散項が誘導する不安定性は、チューリング不安定性と呼ばれます。
であれば det(J)が負になり得ることがわかります。このように拡散項が誘導する不安定性は、チューリング不安定性と呼ばれます。
[edit] 非線形モデル
チューリングモデルは通常、非線形微分方程式として表現されます。
- マインハルトのモデル
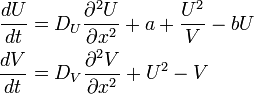
- 川崎のモデル
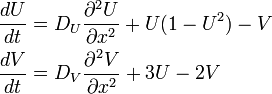
2次の項は活性化因子や抑制因子の生成をシャープにするためです。 とりわけ活性化因子は、パラメータを適切に設定しないと無限大に発散しがちなので、高次項を導入します。
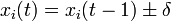
![\begin{align}
\langle x(n)\rangle &= \textstyle\frac{1}{N}\sum^{N}_{i=1}x_i(n) = \frac{1}{N}\sum^{N}_{i=1}x_i(n-1)\pm \delta \\
&= \textstyle\frac{1}{N}\sum^{N}_{i=1}x_i(n-1) = ... = x(0) = 0 \\
\langle x(n)^2\rangle &= \textstyle\frac{1}{N}\sum^{N}_{i=1}x_i(n)^2 = \frac{1}{N}\sum^{N}_{i=1}( x_i(n-1)\pm\delta)^2 \\
&= \textstyle\frac{1}{N}\sum^{N}_{i=1} \Big[x_i(n-1)^2 + \delta^2 \Big]= ... = n\delta^2 \end{align}](/mediawiki/images/math/7/a/7/7a728ad2bd779ffc011c8b13d42661a8.png)
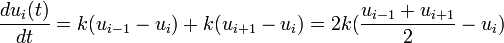
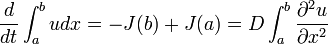
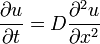
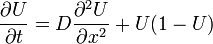
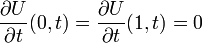
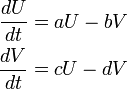
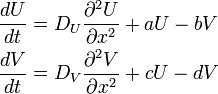
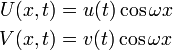
![\begin{align}
\frac{dU}{dt} &= [ (- D_U \omega^2 + a) u - bv ] \cos \omega x\\
\frac{dV}{dt} &= [ cu - (D_V \omega^2 + d) v ] \cos \omega x
\end{align}](/mediawiki/images/math/8/8/c/88cf666caa73bd2b0e2cbfd7f89488aa.png)