Aritalab:Lecture/Math/Resultant
規約多項式と因数分解の一意性
多項式 f が体 k 上で規約であるとは、それ自身が定数ではなく、2つの定数ではない体 k 上の多項式の積にならないことを意味する。定数でない多項式 f は、k 上で規約な多項式の積に分解できる。( f が規約でない場合 f = gh と書くことができ、g, h の全次数は f のそれより小さい。これを繰り返せば、必ず有限回で分解はおわる。)
ここでは規約多項式があたかも素数のように振る舞うことを証明する。
- 定理3
- f が規約な多項式で f が体 k 上の gh を割り切るとき、f は g か h のどちらかを割り切る。
- 証明
変数の個数に関する帰納法を用いる。
- 変数が 1 種類の場合
- p = GCD( f,g ) とおく。p が定数なら(互いに素の場合) Af + Bg = 1 とできる(1章6命題6)。これに h をかけると Bgh は f で割り切れるので、f は h を割り切る。また p が定数でないとき f は規約なので p の定数倍のはずで、g を割り切る。
- 変数が n 種類の場合
- 帰納法の仮定から n - 1 種の変数では仮定は成立。まず f が n 個目の変数 x1 を含まない場合を考える。すると x1 は定数のように扱える。f が g も h も割り切らないとすると、
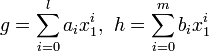
の中で f が ai も bj も割り切らないような最小の添字 i, j が存在する。ここで gh における x1i+j の係数 ci+j を考える。g に含まれる x1 と h に含まれる x1 を掛けあわせて i+j になる部分を取ってくるから
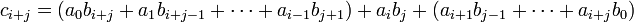
ここで i, j の選び方から ( ) でくくった部分は f で割り切れるが、aibj は割り切らない。よって f は ci+j を割り切らなくなり、f が gh を割り切ることと矛盾する。従って f は g か h のいずれかを割り切る。
次に f が n 個目の変数 x1 を含む一般の場合を考える。ここで、体 k( x2, …, xn ) を係数とする 1 変数の多項式環 k( x2, …, xn )[x1] を考える。この環は k[ x2, …, xn ] の分数を係数にもつので、 k[ x1, …, xn ] は k( x2, …, xn )[x1] に埋め込まれているとみなせる。
まず、この大きな環の中でも f が既約であることを示す。f = AB と分解できる場合、A, B の係数に現れる分母を全て掛けあわせたものを d とおき、d2 f = A'B' と書いてみる (A' = dA, B' = dB)。d は変数 x1 を含まないので、その既約因子を用いて A' か B' を割り切ることができる。そうして残った式は f = A'1 B'1 となるが、f は規約なので A'1 または B'1 は定数である。そしてこれらは A と B に k[ x2, …, xn ] の多項式を掛けたり割ったりしてできているから、A または B は x1 を含んでおらず、f は既約となる。
さて f は k( x2, …, xn )[x1] で既約であり、定理の n=1 の場合に基づき、k( x2, …, xn )[x1] の元として g か h を割り切る。そこで g = A f とおいて分母を払うと
dg = A' f
が k[ x1, …, xn ] の式として得られる。ここで d ∈ k[ x2, …, xn ] のため、d の既約な因子( x1 を含まない)は A' f を割り切る。それを両辺から除いていくと結果として d は消え、f は g を割り切ることがわかる。よって定理は証明された。
- 系4
f, g ∈ k[ x1, …, xn ] が変数 x1 について正の次数をもつとする。このとき、f と g が k[ x1, …, xn ] において x1 に関する正の次数の共通因子をもつことと、k( x2, …, xn)[x1] において共通因子を持つことは同値である。
- 証明
共通因子を持つとき、係数に多項式の分数を含む、より大きな多項式環 k( x2, …, xn)[x1] においても共通因子を持つことは自明。ここでは逆を示す。f と g の共通因子を h と置くと
f = h' f'1, f'1 ∈ k( x2, …, xn)[x1]
g = h' g'1, g'1 ∈ k( x2, …, xn)[x1]
と表される。h', f'1, g'1 は k[ x2, …, xn ] の元を分母に持つかもしれないのでこれらの共通分母 d を式にかけてみる。
d2 f = h f1 d2 g = h g1
ここで h, f1, g1, d は分母の無い k[ x2, …, xn ] の元である。h の規約因子で x1 に関して正の次数を持つものを h1 とする。h' = h / d で x1 に関して正の次数をもつから、そのような因子は必ず存在し、これは f を割りきらねばならない。同様に h1 は g も割り切るので、これが求めていた共通因子である。よって系4は証明された。
- 定理5
定数でない多項式 f ∈ k[ x1, …, xn ] は f = f1 ・ f2 … fr と、規約多項式の積として書ける。おなじ f が f = g1 ・ g2 … gs という多項式の積に分解できるとき r = s であり、gi たちを並べ替えると fi は gi の定数倍となる。
- 証明
有理多項式については、既約多項式への因数分解のアルゴリズムが存在する。実数や複素数を係数にもつ多項式の因数分解は難しい。
終結式
- 補題6
f, g ∈ k[x] がそれぞれ次数 l >0, m >0 を持つとする。このとき f, g が共通因子を持つことと、多項式 A, B ∈ k[x] があって以下の条件をみたすことは同値である。
- A, B はともに 0 ではない。
- A は次数が高々 m-1, B は次数が高々 n-1
- Af + Bg = 0
共通因子 h を持つ場合、因子の次数は少なくとも 1 以上である。 このとき f = h B, g = h (-A) とおけば、AとBは上記の3性質を満たしている。 逆に、上記の3性質を満たす A, B が与えられた時を考える。 もし f, g が共通因子を持たないと仮定するとその最大公約元は 1 になる。 従って多項式 A', B' が存在して
A' f + B' g = 1
を満たす(1章§5の6)。ここで
B = (A' f + B' g) B = A' B f + B' B g = A' B f - B' A f = (A' B - B' A) f
B は 0 ではないので B の次数は少なくとも f と等しいかそれより大きい。 しかしこれは性質 2 に反するので矛盾する。すなわち、 f, g は共通因子を持たねばならない。これで補題6が証明できた。
しかし A, B と書かれた多項式の存在が検証できなくては、共通因子の有無がわからない。そこで Af + Bg = 0 という式を以下の線形方程式系に変換する。
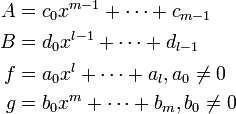
ここで f, g の係数 (ai, bi) は既知、A, B の係数が未知数である。これらを用いて Af + Bg = 0 を作成し、 x のベキの係数を比較してみる。すると l + m 個の方程式と l + m 個の未知数があるため、線形代数を用いて解を求められる。
- 定義7
終結式とは、正の次数を持つ2つの多項式 f, g ∈ k[x] を
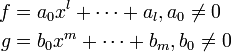
の形に書いて、Af + Bg = 0 に従い x のべき係数を比較する (l+m) x (l+m) 行列(シルベスター行列) Syl(f, g, x) の行列式を指す。これを Res(f, g, x) と書く。
Res(f, g, x) = det( Syl(f, g, x) )
- 命題8
正の次数を持つ2つの多項式 f, g ∈ k[x] が共通因子を持つことは、その終結式 Res(f, g, x) の値が 0 になることと同値である。
- 証明
シルベスター行列の行列式を与える公式をみると、係数行列の行列式がゼロであることは Af + Bg = 0 を満たすような解が存在することに相当する。
- 例
f = 2 x2 + 3x + 1 と g = 7 x2 + x + 3 の終結式を計算すると 0 ではない。よって共通因子は存在しない。
- 命題9
正の次数を持つ多項式 f, g に対し、多項式 A, B で
Af + Bg = Res(f, g, x)
となるものが存在する。
- 証明
Res(f, g, x) = 0 のときは、A = B = 0 とすればよいので自明。 Res(f, g, x) ≠ 0 とする。このとき
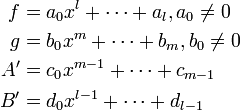
とおく。ここで x のべき係数を比較する(補題6に同じ)。そのとき、x のべき係数が 0 となる項の和が 1 になる以外は補題6の証明に同じである。 実は A' = A / Res(f, g, x), B' = B / Res(f, g, x) という関係になっている。
こう置いてクラメールの公式を用いて唯一の解を与える。クラメールの公式は
![c_i = \frac{1}{Res(f, g, x)} det \Big[ (l+m) \times (l+m) matrix\Big]](/mediawiki/images/math/d/f/a/dfac591ccc0a8d8e7fe3bcd8245b6cc9.png)
であるから、Res(f, g, x) を全体にかければ ci は ai, bi からなる整数係数多項式になる。